Question

Timber beams are widely used in home construction. When the load​ (measured in​ pounds) per unit length has a constant value over part of a​ beam, the load is said to be uniformly distributed over that part of the beam. Consider a cantilever beam with a uniformly distributed load between 90 and 105 pounds per linear foot. a. What is the probability that a beam load exceeds 99 pounds per linear​ foot? b. What is the probability that a beam load is less than 92 pounds per linear​ foot? c. Find a value L such that the probability that the beam load exceeds L is 0.4.

Answer 1

a) 0.4

b) 0.133

c)
`L \geq 99`

Explanation:

We are given the following information in the question:

The load is said to be uniformly distributed over that part of the beam between 90 and 105 pounds per linear foot.

a = 90 and b = 105

Thus, the probability distribution function is given by

`f(x) = \displaystyle(1)/(b-a) = (1)/(105-90) = (1)/(15),\\\\90 \leq x \leq 105`

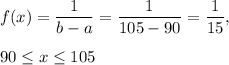
a) P( beam load exceeds 99 pounds per linear​ foot)

P( x > 99)

`=\displaystyle\int_(99)^(105) f(x) dx\\\\=\displaystyle\int_(99)^(105) (1)/(15) dx\\\\=(1)/(15)[x]_(99)^(105) = (1)/(15)(105-99) = 0.4`

b) P( beam load less than 92 pounds per linear​ foot)

P( x < 92)

`=\displaystyle\int_(90)^(92) f(x) dx\\\\=\displaystyle\int_(90)^(92) (1)/(15) dx\\\\=(1)/(15)[x]_(90)^(92) = (1)/(15)(92-90) = 0.133`

c) We have to find L such that

`\displaystyle\int_(L)^(105) f(x) dx\\\\=\displaystyle\int_(L)^(105) (1)/(15) dx\\\\=(1)/(15)[x]_(L)^(105) = (1)/(15)(105-L) = 0.4\\\\\Rightarrow L = 99`

The beam load should be greater than or equal to 99 such that the probability that the beam load exceeds L is 0.4.