Question

Biomedical laboratories routinely use ultracentrifuges, some of which are able to spin at 1.00 × 10 5 rev/min about the central axis. The turning rotor in certain models is about 20.0 cm in diameter. At its top spin speed, what force does the rotor exert on a 2.00-g sample that is positioned at the greatest distance from the spin axis? Would the force be appreciably different if the sample were spun in a vertical or a horizontal circle? Why or why not?

Answer 1

21.932 kN

Step-by-step explanation:

Given:

Angular velocity, ω = 1.00 × 10⁵ rev/min

Diameter of the turning rotor = 20.0 cm = 0.2 m

or

Radius, r =
`\frac{\textup{0.2}}{\textup{2}}` = 0.1 m

Mass of the sample = 2.00 g = 0.002 Kg

Now,

Force = mass × ω² × r

Here,

ω = 100000 rev/min

or

ω =
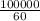`\frac{\textup{100000}}{\textup{60}}` rev/sec

or

ω = 1667.67 rev/sec

also,

ω = 1667.67 × 2π = 10471.97 radian/s

Therefore,

force = 0.002 × 10471.97 × 0.1

or

Force = 21932.43 N

or

Force = 21.932 kN

b) No the force would not be different as it does not depend on the axis of rotation as it can be observed in the formula

Force = mass × ω² × r