Answer:
With 95% confidence, mean nightly hours of sleep for all college student is between 5,9616 and 6,4384 hours.
Step-by-step explanation:
Sample mean of sleeping hours of randomly selected 50 college students deviates from the mean of sleeping hours of all college students. We need to calculate margin of error for the sample mean to make an estimate for all college students.
 The general formula for the margin of error for the sample mean is
The general formula for the margin of error for the sample mean is
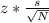
 where z is the appropriate z-value for your desired level of confidence (for 95% it is approximately 1.96), s is the sample standard deviation (in fact it is population standard deviation but it is replaced when this value is unknown), and N is the sample size.
where z is the appropriate z-value for your desired level of confidence (for 95% it is approximately 1.96), s is the sample standard deviation (in fact it is population standard deviation but it is replaced when this value is unknown), and N is the sample size.
 Then our formula becomes
Then our formula becomes
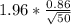 which is equal to 0.2383798
which is equal to 0.2383798
 As a result, with 95% confidence, hours of sleep of all college students in average is between 6.2-0.2383798 and 6.2+0.2383798, ie between 5,9616 and 6,4384 hours.
As a result, with 95% confidence, hours of sleep of all college students in average is between 6.2-0.2383798 and 6.2+0.2383798, ie between 5,9616 and 6,4384 hours.