Answer:
The flux decreases because the angle between B⃗ and the coil's axis changes.
Step-by-step explanation:
The flux through the coil is given by a dot product, between the magnetic field and the vector representing the area of the coil.
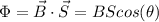
The latter vector has direction perpendicular to the plane in which the area of the coil is, and magnitude equal to the area of the coil. As in the attached image, the vector S is the vector respresenting the area of the coil.
Therefore, the flux will be maximum when the vector S is in the same direction as B, and will be zero when they are perpendicular.
Now, if the coil is rotated so that the magnetic field is in the plane of the coil then, the vectors S and B are perpendicualr, and there will not be net magnetic flux, that is, the flux will decrease.