Answer:
F(M) = 0.7 F(N)=0.3
Step-by-step explanation:
We need to take into account that individuals NN and MM only N or M aleles respectively while MN gives just half of the allelic contribution for each. With this in mind we have the following probabilities for getting each of the alleles: MM => p(M) = 1.0 and p(N)=0.0
MN => p(M ) = 0.5 and p(N) = 0.5
NN => P(M) = 0.0 and p(N) = 1.0
With this we can calculate the frequencies of the M and N alleles in the population with 100 individuals using the following formulas
For f(M):
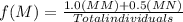
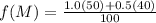
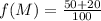
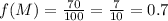
The frequency of the M allele is 0.7
For f(N):
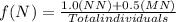
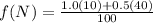
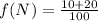
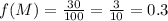
The frequency of the N allele is 0.3