Question

You are a researcher studying the lifespan of a certain species of bacteria. From a previous study, it was found that the standard deviation was 5.2 hours. You would like to estimate the mean lifespan for this species of bacteria to within a margin of error of 0.65 hours at a 99% level of confidence. What sample size should you gather to achieve a 0.65 hour margin of error? Round your answer up to the nearest whole number.

Answer 1

Answer: 425

Explanation:

As considering the given description, we have

Population standard deviation:
`\sigma=5.2`

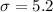
Margin of error : E = 0.65

Critical value for 99% confidence interval :
`z_(\alpha/2)=2.576`

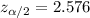
Formula to find the sample size :
`n=((z_(\alpha/2)\cdot \sigma)/(E))^2`

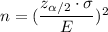
i.e.
`n=(((2.576)\cdot (5.2))/(0.65))^2`

`=(20.608)^2=424.689664\approx425`

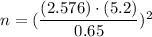
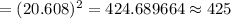
Hence, the required minimum sample size =425