Question

Marion rides her racing bicycle at a speed of 8 m/s. The bicyle wheels have a radius of 34 cm.

A. What is the angular speed of the wheels?
B. How many times does each wheel go around during a 10 minute ride?

Answer 1

Part A) The angular speed of the wheels is
`23.53(rad)/(sec)`

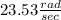
Part B) Approximately 2,247 revolutions

Step-by-step explanation:

Part A) What is the angular speed of the wheels?

we know that

The Angular speed is equal to divide the Linear speed by the radius

Let

s -----> the linear speed in m/sec

r -----> radius in m

w ----> angular speed in rad/sec

`w=(s)/(r)`

we have

`s=8\ m/sec\\r=34\ cm=34/100=0.34\ m`

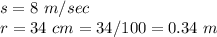
substitute

`w=(8)/(0.34)`

`w=23.53(rad)/(sec)`

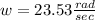
Part B) How many times does each wheel go round during a 10-minute ride?

we know that

As the wheel rotates one time, a point on the wheel rotates 2π radians.

Remember that

`10\ minutes = 600\ seconds`

`\theta = w * t = ((8)/(0.34)) * 600= (4,800)/(0.34)\ radians`

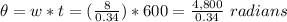
To find out the number of rotations divide by 2π

`((4,800)/(0.34))/(2\pi)=2,246.9`

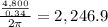
Approximately 2,247 revolutions