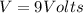When a 100-Ω resistor is connected across the terminals of a battery of emf ε and internal resistance r, the battery delivers 0.794 W of power to the 100-Ω resistor. When the 10…

Question

asked Dec 7, 2020 3.3k views

1 Answer

Scottalan · Answer 1 · 2020-12-11T18:36:49+0000

Answer:

(E) ε = 9.00 V, r = 1.01 Ω

Step-by-step explanation:

As we know that power across the resistance is given as

P = i^2 R

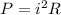
now we will have

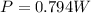
P = 0.794 W

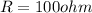
R = 100 ohm

now we have

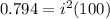
0.794 = i^2(100)

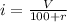
i = (V)/(100 + r)

now we can use it as

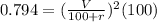
0.794 = ((V)/(100 + r))^2(100)

similarly now 100 ohm resistance is replaced by another resistance of 200 ohm

so we will have

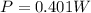
P = 0.401 W

R = 200 ohm

now we have

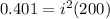
0.401 = i^2(200)

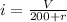
i = (V)/(200 + r)

now we can use it as

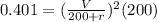
0.401 = ((V)/(200 + r))^2(200)

now we have

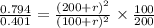
(0.794)/(0.401) = ((200 + r)^2)/((100 + r)^2)* (100)/(200)

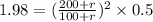
1.98 = ((200 + r)/(100 + r))^2 * 0.5

1.99 = (200 + r)/(100 + r)

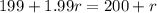
199 + 1.99 r = 200 + r

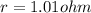
r = 1.01 ohm

now to find voltage of cell we will have

V = 9 Volts