Answer:
49% of employees who either have MBA or are managers.
Explanation:
We are given the following information in the question:
P(Managerial) = 35% = 0.035
P(MBA) = 67% = 0.67
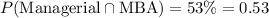
We have to find the probability of employees who either are have MBA or are managers.
According to De-Morgan's law:
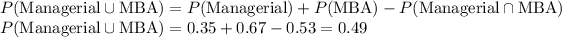
Thus, around 49% of employees who either have MBA or are managers.