Question

A certain neutron star has five times the mass of our Sun packed into a sphere about 10 km in radius.

Answer 1

the answer is 5.5x10^12 but i keep getting 6.06x10^16

i am using g = GM2/r^2

Step-by-step explanation:

Answer 2

The surface gravity of the neutron star is
`g = 6.63x10^(12)m/s^(2)`

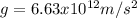
Step-by-step explanation:

To determine the value surface gravity is necessary to combine the equation of the weight and the equation for the Universal law of gravity:

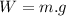`W = m.g` (1)

Where m is the mass and g is the value of the gravity

`F = G (M.m)/(R^(2))` (2)

Equation (1) and equation (2) will be equal since the weight is a force acting on the object as a consequence of gravity:

`m.g = G (M.m)/(R^(2))` (3)

Then g will be isolated from equation 3:

`g = G (M.m)/(m.R^(2))`

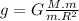
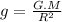`g = (G.M)/(R^(2))` (4)

The mass of the Sun has a value of
`1.989x10^(30) kg`

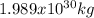
Therefore, the mass of the neutron star will be:

`m_(nstar) = 5(1.989x10^(30) kg)`

`m_(nstar) = 9.945x10^(30) kg`

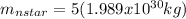
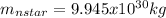
Finally, equation 4 can be used:

`g = ((6.67x10^(-11) N.m^(2)/kg^(2))(9.945x10^(30)kg))/((10000m)^(2))`

`g = 6.63x10^(12)m/s^(2)`

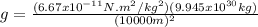
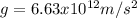
Hence, the surface gravity of the neutron star is
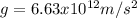`g = 6.63x10^(12)m/s^(2)`.