Question

Seven identical model truss bridges are constructed. Each is loaded with increasing masses until it collapses. The masses used are in 50g increments. The loads at failure are 1.40 kg, 1.40 kg, 1.45 kg, 1.50 kg, 1.55 kg, 1.60 kg, and 1.60 kg. If an additional truss is constructed, estimate with 95 % confidence the loaded mass at which the truss will fail.

Answer 1

With 95% confidence, estimate loaded mass at which the additional truss will fail falls between 1.4258 and 1.5742 kg. Because the masses are used in 50g increments, our interval is between 1.45 and 1.60 kg

Explanation:

Seven loads of failure are measured. Let S be the sample of these values, then

`\\`S={1.40, 1.40, 1.45, 1.50, 1.55, 1.60, 1.60}

`\\`Size of the sample, N=7

`\\`Mean of the sample, M=1.50

`\\`Standard Deviation of the sample, s =0.0802

`\\`To estimate the loaded mass at which the additional truss will fail with 95% confidence, we need to calculate the margin of error for the sample mean.

`\\`Confidence interval for the estimate would be

`\\`M±
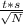`(t*s)/(√(N) )` where M is the mean of the sample, t is the appropriate t-value for 95% level of confidence, s is the sample standard deviation and N is the sample size.

Since our sample is small (<30), we'll use corresponding t-table value for 95% confidence level and 6 (M-1) degrees of freedom, which is 2.447

Our formula becomes 1.50±
`(2.447*0.0802)/(√(7) )`

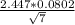
i.e 1.50±0.0742

Therefore estimate loaded mass at which the additional truss will fail falls between 1.4258 and 1.5742 kg. Because the masses are used in 50g increments, our interval is between 1.45 and 1.60 kg