Question

At a certain fast-food restaurant, 65% of customers order a chicken sandwich, 44% of customers order french fries, and 76% of customers order a chicken sandwich or french fries (or both items). What is the probability that a randomly selected customer will order both a chicken sandwich and french fries? Write your answer as a decimal (not as a percentage). (If necessary, consult a list of formulas.)

Answer 1

Answer: 0.33

Explanation:

Let C be the event of ordering chicken sandwich.

F be the event of ordering french fries.

As per given , we have

P(C)=0.65

P(F)=0.44

P(C∩F)=0.76

Formula we use here,
`P(A\cap B)=P(A)+P(B)-P(A\cup B)`

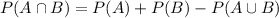
Then, For given situation, we have

`P(C\cap F)=P(C)+P(F)-P(C\cup F)`

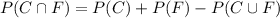
i.e.
`P(C\cap F)=0.65+0.44-0.76=0.33`

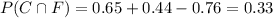
Hence, the probability that a randomly selected customer will order both a chicken sandwich and french fries=0.33