Question

Find the distance from the point
`(6, 4)` to the line
`y=x+4`.

Answer 1

Hey!

-------------------------------------------------

First, we need to find the second coordinate.

`\text{We know that the slope is 1 and the y-intercept is 4.}\\\text{We use}~(1 - 4)/(x - 6) = 1~\text{to solve for x.}\\\text{We can simplify this to}~(-3)/(x-6)\\\text{Now we know that whatever x subtracts to 6 we get -3 to get a slope of 1.}\\\text{After solving we can use 3 for x.}\\\text{We subsitute for x and end of getting}~(-3)/(-3)~\text{which equals 1.}\\\text{The second point is (3, 4)}`

-------------------------------------------------

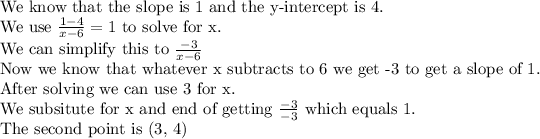
Second, we need to find the distance between both points.

`d = √((3 - 6)^2 + (1 - 4)^2) \\d = √((-3)^2 + (-3)^2) \\d = √(9+9) \\d = √(18) \\\text{We can simplify this using what we know about radicals.}\\d = 3√(2)`

-------------------------------------------------

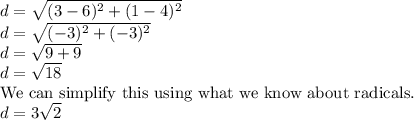
Hence, the answer is
`3√(2)`!

-------------------------------------------------

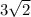Hope This Helped! Good Luck!

Answer 2

`\large \boxed{3√(2)}`

Explanation:

1. Express the line in standard form.

ax + by + c = 0

`\begin{array}{rcl}y & = & x + 4\\-x + y - 4 & = & 0\\\end{array}`

2. Calculate the distance

The formula for the distance d from a point (x, y) and the line is:

`d = \fracax + by + c{\sqrt{a^(2) + b^(2)}}`

Insert the values: a = -1; b = 1; c = -4; x = 6; y = 4

`\begin{array}{rcl}d &= &\frac{\sqrt{(-1)^(2) + 1^(2)}}\\\\& = & (|-6 + 4 - 4|)/(√(1 + 1))\\\\& = & (|-6|)/(√(2))\\\\& = &(6)/(√(2))\\\\& = & (3*√(2)*√(2))/(√(2))\\\\& = & \mathbf{3{√(2)}}\end{array}\\\text{The distance from the point to the line is $\large \boxed{\mathbf{3√(2)}}$}`