Question

Given f(x) =4x^4 + 5x^3 - 15x^2 -45, find f(-3)

Answer 1

When evaluated at x = -3, the function
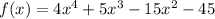`f(x) = 4x^4 + 5x^3 - 15x^2 - 45` takes the value 9.

Step-by-step explanation:

To find f(-3), we simply substitute x = -3 into the function's expression:

`f(-3) = 4(-3)^4 + 5(-3)^3 - 15(-3)^2 - 45\\f(-3) = 4 * 81 + 5 * -27 - 15 * 9 - 45\\f(-3) = 324 - 135 - 135 - 45\\f(-3) = 324 - 285\\f(-3) = 9`

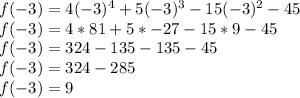
Therefore, f(-3) = 9.

In conclusion, evaluating f(x) at x = -3 reveals its value as 9. This demonstrates that even negative inputs can yield positive function outputs, highlighting the dynamic nature of polynomial expressions. While finding f(-3) may seem like a simple substitution, it reinforces the importance of understanding the underlying function's structure and applying basic algebraic principles.

Answer 2

Yeah I always saw it as he was writing the history book he always wished he had