Question

A rocket is launched at an angle of 38o above the horizontal with an initial speed of 78 m/s. It moves for 3 s along its initial line of motion with an acceleration of 12 m/s2 . At this time, its engines fail and the rocket then moves as a projectile. Find the maximum height of the rocket and the horizontal range (distance from launch point to landing point).

Answer 1

y = 428.67 m and x all = 1513.68 m

Step-by-step explanation:

This problem of kinematics can be divided into two parts: a first part when the rockets work a second as a parabolic launch.

Let's do the first part, let's calculate the speed just when the engines turn off

vf = v₀ + at

vf = 78 + at

vf = 78 +12 3

vf = 114 m / s

This is the speed with which the second part begins vo = 114 m / s with an Angle of 38º

Also at this time a distance is displaced, we calculate the distance traveled (in the direction of the acceleration)

d = v₀ t + ½ a t²

d = 78 3 + ½ 12 3²

d = 288 m

Let's use trigonometry to find the components

x₀ = d cos 38 = 288 cos 38

y₀ = d sin38 = 288 sin38

x₀ = 226.95 m

y₀ = 177.31 m

Second part

Let's calculate the maximum height, at this point its vertical speed is zero (vfy = 0)

Let's decompose the initial velocity using trigonometry

vₓ = v₀ cos 38

`v_(y)` = v₀ sin38

vₓ = 114 cos 38

`v_(y)` = 114 sin38

vₓ = 89.83 m / s

`v_(y)` = 70.19 m / s

`v_(fy)`² =
`v_(oy)`² - 2g (y -y₀)

0 =
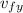`v_(oy)`² -2g (y -yo)

y-y₀ =
`v_(oy)`² / 2g

y-y₀ = 70.19²/2 9.8

y = 251.36 + y₀

y = 251.36 + 177.31

y = 428.67 m

This is the maximum height from the point where the movement began, that is, the ground.

Now let's calculate the range

R = vo² sin 2θ / g

R = 114² sin 2 38 /9.8

R = 1286.73 m

This is the scope of the parabolic movement, we must add the horizontal distance traveled in the first part

x all = R + xo

x all = 1286.73 + 226.95

x all = 1513.68 m