Question

Jallouk Corporation has two different bonds currently outstanding. Bond M has a face value of $70,000 and matures in 20 years. The bond makes no payments for the first six years, then pays $2,800 every six months over the subsequent eight years, and finally pays $3,100 every six months over the last six years. Bond N also has a face value of $70,000 and a maturity of 20 years; it makes no coupon payments over the life of the bond. The required return on both these bonds is 10 percent compounded semiannually.

Answer 1

Bonds N present market value: $ 10,405.05

Bond M present market value: $ 36.893,9‬0

Step-by-step explanation:

Bond N is a zero-coupon we discount maturity at 10%:

We calculate using the present value of a lump sum:

`(Maturity)/((1 + rate)^(time) ) = PV`

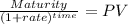
Maturity 70,000.00

time 20.00

rate 0.1

`(70000)/((1 + 0.1)^(20) ) = PV`

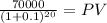
PV 10,405.05

Bond M

present value of the annuity payment:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 2,800.00

time 16 (8 years 2 payment per year)

rate 0.05 (10% annual becomes 5% semiannual)

`2800 * (1-(1+0.05)^(-16) )/(0.05) = PV\\`

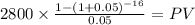
PV $30,345.7548

Then we discount at present date using the lump sum formula:

`(30345.7547684816)/((1 + 0.05)^(16) ) = PV`

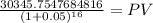
PV 13,901.74

We do the same for the next annuity:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 3,100.00

time 12

rate 0.05

`3100 * (1-(1+0.05)^(-12) )/(0.05) = PV\\`

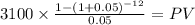
PV $27,476.0801

`(27476.0800729913)/((1 + 0.05)^(16) ) = PV`

PV 12,587.11

Now we add the present valeu of the maturity: which is the value of the zero-coupon bond: 10,405.05

Bond M present value: 10,405.05 + 12,587.11 + 13,901.74 = 36.893,9‬