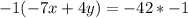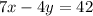Answer:
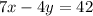
Explanation:
Given
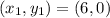
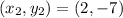
Required
Determine the equation in standard form
First, calculate the slope (m) using:
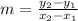
This gives:
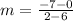
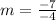

The equation in standard form is calculated using:
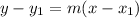
This gives:
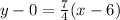
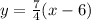
Cross Multiply
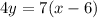
Open bracket
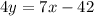
Subtract 7x from both sides
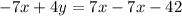
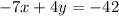
Multiply through by -1