Question

A college professor never finishes his lecture before the end of the hour and always finishes his lectures within 2 min after the hour. Let X = the time that elapses between the end of the hour and the end of the lecture and suppose the pdf of X is as follows. f(x) = kx2 0 ≤ x ≤ 2 0 otherwise (a) Find the value of k. (Enter your answer to three decimal places.)

Answer 1

Value of k is
`\displaystyle(3)/(8)`

Explanation:

We are given the following information in the question:

`f(x) = kx^2, 0\leq x \leq 2\\~~~~~~~= 0, \text{ otherwise}`

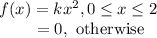
where x is the time elapses between the end of the hour and the end of the lecture.

We have to find the values of k.

Since, f(x) is the pdf, then,

`\displaystyle\int^\infty_(-\infty) f(x) = 1\\\\\displaystyle\int^2_(0) f(x) = 1\\\\\displaystyle\int^2_(0) kx^2 = 1\\\\k\bigg[(x^3)/(3)\bigg]^2_0 = 1\\\\k* (8)/(3) = 1\\\\k = (3)/(8)`

Hence, value of k is
`\displaystyle(3)/(8)`