Answer:
Ater 3 minute
product =
 Molar
Molar
susbtrate = 0.081%
after 5.3 minutes
product =

susbtrate = 0.01435
Step-by-step explanation:
Given data:
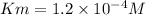
Sustrate concentration = 0.02 M
Amount of product
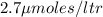
Rate = dP/dT = product formed per time
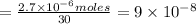
we know rate
![= (v_(max)[S])/(Km + S)](https://img.qammunity.org/2020/formulas/physics/college/u8xp9l4w80upfenr8o4biwzjuy1bwcid17.png)
hence
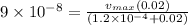
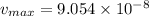
now after 3 min = 180 sec
product formed
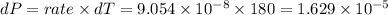 Molar,
Molar,
% substrate utilised
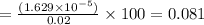 %
%
after 3.5 minutes = 318
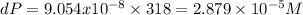
%
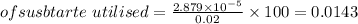 %
%