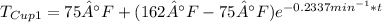Answer:
The equations of both cups after t minutes is given by:
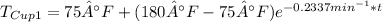
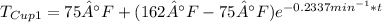
Explanation:
The complete exercise says:
Two cups of coffee are poured from the same pot. The initial temperature of the coffee is 180°F, and is 0.2337 (for time in minutes).
Newton's law of cooling:
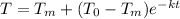
where,
 = room temperature
= room temperature
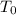 = initial temperature
= initial temperature
k=cooling constant
Hence,
Cup 1:
 = 75 °F
= 75 °F
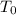 = 180 °F
= 180 °F
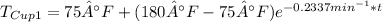
Cup 2:
 = 75 °F
= 75 °F
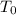 = 162 °F
= 162 °F