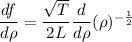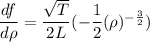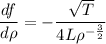Answer:
(i)
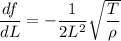
(ii)
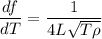
(iii)
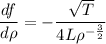
Explanation:
Let as consider the frequency (in Hz) of a vibrating violin string is given by
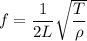
(i)
Differentiate f with respect L (assuming T and rho are constants).
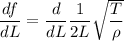
Taking out constant terms.
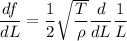
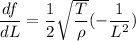
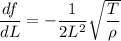
(ii)
Differentiate f with respect T (assuming L and rho are constants).
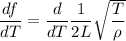
Taking out constant terms.
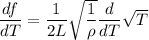

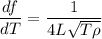
(iii)
Differentiate f with respect rho (assuming L and T are constants).

Taking out constant terms.