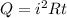Answer: 137.76 A
Explanation: Heat is generated in a material when current is passed through the conducting material, this process is known as Joule heating or Ohmic heating or resistive heating.
Joule's first law, also known as Joule-Lenz law states that the heating power generated by an electrical conductor is directly proportional to the resistance of the conductor and square of the current flowing through it.
Mathematically, we have:
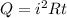 ...............................(1)
...............................(1)
where:
- i= current flowing through the conductor
- R= resistance of the conductor
- t= time for which the current flows in the conductor
GIven data:
- heat required for the vapourization of water into steam, L 2256
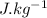
- heat of vaporization per kg of water,
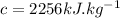
- density of water,
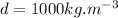
- time for which the current flows= 2.14 ms =
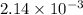 s
s
- resistivity of water,
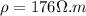
- lenght of water along which the current flows,
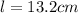
- vertical cross-section area which is normal to the direction of current flow,
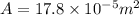
To find:
- The current required to vaporize the given water, i = ?
Firstly, we calculate the amount of energy required by the given amount of water to vaporize.
We have the density and heat of vaporization per kg of water.
volume of water=
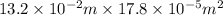
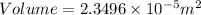
Now, Mass of water
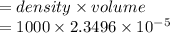
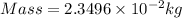
∴Total amount of heat energy required,
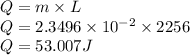
we know, resistance
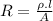
Putting the given values

Using eq. (1)