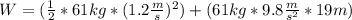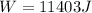Question

At the corner of the SBCC campus there is a walking path with a big staircase. There are 126 steps that are an average height of 15 cm (for each step). A 135 lbs. woman climbs the stairs. She starts from rest and is moving 1.2 m/s at the top (a walking pace). How much work does she do? You might want to look at Example 7.11: Calculating the Power to Climb Stairs for reference.

Answer 1

The work done is
`W=11403J`

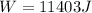
Step-by-step explanation:

1. Define the formula of work.

In this case the work (W) done is the result of add up the kinetic energy
`K_(E)` and the potential energy
`K_(E)`, and subtract them at the initial and final states:

`W=(K_(Ef)+P_(Ef))-(K_(Ei)+P_(Ei))`

`K_(E)=(1)/(2)mv^(2)`

`P_(E)=mgh`

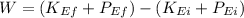
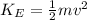
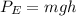
Replacing expressions:

`W=((1)/(2)mv_(f)^(2)+mgh_(f))-((1)/(2)mv_(i)^(2)+mgh_(i))`

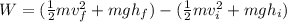
In the initial state at the bottom of the stairs both kinetic and potential energy are equal to zero, because kinetic energy depends on velocity and her initial velocity is zero, and potential energy depends on height and her initial height is zero too.

So the work done is defined by:

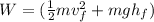`W=((1)/(2)mv_(f)^(2)+mgh_(f))` (Eq.1)

2. Calculate the height:

`126steps*(15cm)/(1step)*(1m)/(100cm)=19m`

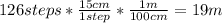
The height of the stairs is 19m

3. Convert the mass of the woman from lbs to kg:

`135lbs*(0.45kg)/(1lb)=61kg`

The woman heights 61kg

4. Replace values in (Eq.1):

`W=((1)/(2)*61kg*(1.2(m)/(s))^(2))+(61kg*9.8(m)/(s^(2))*19m)`

`W=44kg(m^(2))/(s^(2))+11359kg(m^(2))/(s^(2))`

`W=11403J`