Answer:
Mrs. Maroney should choose plan 1
Explanation:
Plan 1:
Plan 1 includes walking a dog once a day for a rate of $5 per day.
In 2 weeks (14 days), Jayden will earn
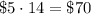
Plan 2:
Plan 2 also includes one walk a day but charges 1 cent for 1 day, 2 cents for 2 days, 4 cents for 3 days, and 8 cents for 4 days and continues to double for each additional day.
So,
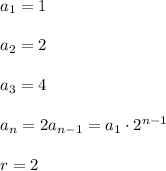
Hence,
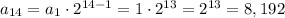
Find the sum
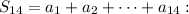
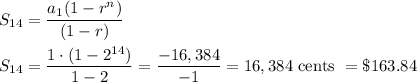
Since $70<$163.84, Mrs. Maroney should choose plan 1