Question

According to sales information in the first quarter of 2015, 2.7% of the new vehicles sold in the United States were hybrids. This is down from 3.3% for the same period a year earlier. An analyst's review of the data indicates that the reasons for the sales decline include the low price of gasoline and the higher price of a hybrid compared to similar vehicles. Let’s assume these statistics remain the same for 2016. That is, 2.7 percent of the new car sales are hybrids in the first quarter of 2016. For a sample of 40 vehicles sold in the Richmond, Virginia, area:

a. How many vehicles would you expect to be hybrid? (Round your answer to 2 decimal places.)

Answer 1

You should expect 1.08 vehicles to be hybrid.

Explanation:

For each vehicle, there are only two possible outcomes. Either it is a hybrid, or it is not. The probability of a vehicle being a hybrid is independent of other vehicles. So we use the binomial probability distribution to solve this question.

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

The expected value of the binomial distribution is:

`E(X) = np`

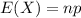
2.7 percent of the new car sales are hybrids in the first quarter of 2016.

This means that
`p = 0.027`

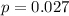
For a sample of 40 vehicles sold in the Richmond, Virginia

This means that
`n = 40`

For a sample of 40 vehicles sold in the Richmond, Virginia

`E(X) = np = 40*0.027 = 1.08`

You should expect 1.08 vehicles to be hybrid.

Answer 2

2 vehicles would be hybrid.

Explanation:

Consider the provided information.

40 vehicles sold in the Richmond, and 2.7% of the new vehicles sold in the United States were hybrids.

Therefore n=40 and π=0.027

Now we need to find vehicles expect to be hybrid.

`\mu=n* \pi`

`\mu=40* 0.027`

`\mu=1.08\approx 2`

Hence, 2 vehicles would be hybrid.