Question

Renna pushes the elevator button, but the elevator does not move. The mass limit for the elevator is 450 kilograms (kg), but Renna and her load of identical packages mass a total of 620 kg. Each package has a mass of 37.4 kg.

1. Write an inequality to determine the number of packages, p, Renna could remove from the elevator to meet the mass requirement.

2. What is the minimum whole number of packages Renna needs to remove from the elevator to meet the mass requirement?

Answer 1

1.
`620-37.4p\leq 450`

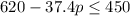
2. 5 packages.

Explanation:

Let p represent number of packages.

We have been given that each package has a mass of 37.4 kg. So mass of p packages would be
`37.4p`.

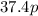We have been given that the mass limit for the elevator is 450 kilograms (kg), but Renna and her load of identical packages mass a total of 620 kg.

The weight of identical packages minus weight of p packages should be less than or equal to mass limit of the elevator. We can represent this information i an inequality as:

`620-37.4p\leq 450`

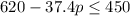
Therefore, the inequality
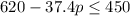`620-37.4p\leq 450` can be used to determine the number of packages that Renna could remove from the elevator to meet the mass requirement.

Let us solve for p.

`620-620-37.4p\leq 450-620`

`-37.4p\leq -170`

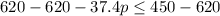
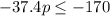
Divide by negative and swap the inequality sign:

`(-37.4p)/(-37.4)\geq (-170)/(-37.4)`

`p \geq 4.54545`

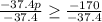
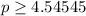
Since Renna cannot remove 0.54 of a package, therefore, the minimum whole number of packages that Renna needs to remove from the elevator would be
`5`.