Answer:
The probability of juniors whose score is at or below =0.1587
The percentage of juniors whose score is at or below 66
P(X≤ 66) = 0.1587 = 15 percentage
Explanation:
Explanation:-
Given mean of the Population (μ) = 73
Given standard deviation of the Population(σ) = 7
Let 'X' be the random variable in normal distribution
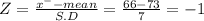
The probability of juniors whose score is at or below 66

= 1 - P( Z>Z₁ )
= 1-( 0.5 +A( Z₁)
= 0.5 - A(-1)
= 0.5 - A(1) (∵ A(-1) = A(1))
= 0.5 - 0.3413
= 0.1587
The probability of juniors whose score is at or below 66
 = 0.1587
= 0.1587
The percentage of juniors whose score is at or below 66
P(X≤ 66) = 15 %