Answer: 0.1
Explanation:
Let F = must stop at first signal .
F’ = do not have to stop at first signal .
S = must stop at second signal .
S’ = do not have to stop at second signal.
As given , we have
P(F)=0.40
P(S)=0.50
P(F∪S)=0.60
Use formula ,

i.e.
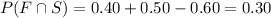
The probability that she must stop at the first signal but not the second signal :
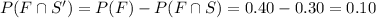
Hence, the probability that she must stop at the first signal but not the second signal= 0.1