Question

A shipping company handles containers in three different sizes: (1) 27 ft3 (3 × 3 × 3), (2) 125 ft3, and (3) 512 ft3. Let Xi (i = 1, 2, 3) denote the number of type i containers shipped during a given week. With μi = E(Xi) and σi2 = V(Xi), suppose that the mean values and standard deviations are as follows: μ1 = 210 μ2 = 250 μ3 = 120 σ1 = 10 σ2 = 13 σ3 = 6 (a) Assuming that X1, X2, X3 are independent, calculate the expected value and variance of the total volume shipped. [Hint: Volume = 27X1 + 125X2 + 512X3.]

Answer 1

E(volume) = 98,360

V(Volume) = 12,150,709

Step-by-step explanation:

The Expected value and Variance have the following properties:

E(aX)=aE(X)

E(X+Y)) = E(X) + E(Y)

V(aX) =
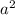`a^(2)`V(X)

V(X + Y) = V(X) + V(Y)

Where X and Y are independent variables and a is constant.

So, The expected value of the total volume is:

E(Volume) = E(27X1 + 125X2 + 512X3)

E(Volume) = E(27X1) + E(125X2) +E(512X3)

E(Volume) = 27E(X1) + 125E(X2) +512E(X3)

E(Volume) = 27μ1 + 125μ2 + 512μ3

E(Volume) = 27(210) + 125(250) + 512(120)

E(Volume) = 98,360

At the same way the variance of the total volume is:

V(Volume) = V(27X1 + 125X2 + 512X3)

V(Volume) = V(27X1) + V(125X2) +V(512X3)

`V(Volume)=(27^(2))V(X1)+(125^(2))V(X2)+(512^(2))V(X3)`

V(Volume) = 729V(X1) + 15,625V(X2) + 262,144V(X3)

V(Volume) = 729(σ1)^2 + 15,625(σ2)^2 + 262,144(σ3)^2

V(Volume) = 729(10)^2 + 15,625(13)^2 + 262,144(6)^2

V(Volume) = 729(100) + 15,625(169) + 262,144(36)

V(Volume) = 12,150,709