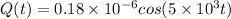Question

A series circuit has a capacitor of 0.04×10−6 F and an inductor of 1 H. If the initial charge on the capacitor is 0.18×10−6C and there is no initial current, find the charge Q on the capacitor at any time t. Enter an exact answer. Do not use thousands separator in the answer field. Enclose arguments of functions in parentheses. For example, sin(2x).

Answer 1

`Q(t) = 0.18* 10^(-6) cos(5* 10^3 t)`

Step-by-step explanation:

We knwo that Kirchoff law

`L(DI(t))/(dt) + (1)/(C)Q = 0`

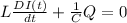
where

`I(t) = (dQ)/(dt)`

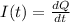
hence

`LQ`

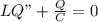
C is given as 0.04\times 10^{6} F

L= 1 H , so we have

`Q`

the characteristic equation of this differential equation is

`r^2 + 25* 10^6 = 0`

`r = \pm 5* 10^3 i`

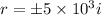
Therefore differential equation is

`Q(t) =  c_1 cos(5000t) + c_2sin(5000t)`

we know initial value if capacitor is given as
`0.18* 10^(-6) C`

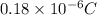
Therefore

`0.18* 10^(-6) = Q(0) =  c_1 cos(0) + c_2sin(0)`

`c_1 = 0.18* 10^(-6)`

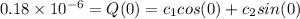
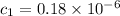
if no inital current is present then we hvae I(0) = Q'(0) = 0

`Q'(T) = -5000 C_1 sin(5000t) +  5000 c_2cos(5000t)`

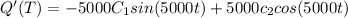
`0 = Q'(0) = - 5000c_1sin(0) + 5000c_2cos(0)` therefre

`c_2 =0`

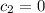
hence charge is

`Q(t) = 0.18* 10^(-6) cos(5* 10^3 t)`