Answer:
P (average within 10) = 0.9984
Explanation:
Given:
Number of consecutive shoppers observed, n = 40
Standard deviation, σ = $21.51
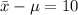
Now,
Standard error (SE) =

or
Standard error (SE) =

or
Standard error (SE) = 3.40
also,
z =

on substituting the values, we have
z =
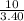
or
z = 2.94
Now, from the Table of Area Under Standard Noral Curve
for z = 2.94 ; area = 0.9984
we have P (average within 10) = 0.9984