Answer:
The Answer is 76.
Explanation:
Given the normal distribution " 10% of employees (rated) exemplary, 20% distinguished, 40% competent, 20% marginal, and 10% unacceptable'', we can see that exemplary employees are top 10% rated employees.
We have the formula for normal distribution:
z=(X-M)÷σ
where z is the minimum z-score for top 10% employee, X is the minimum score for top 10% employee, M is the mean of the score distribution, σ is the standard deviation of the score distribution.
The z-score we are looking for is the value "a" that separates the highest 10% from the lowest 90% i.e. P(z≤a)=0.90
If we look at z-table, corresponding value for a is 1.28155
We can now put the values in the formula:
1.28155=
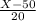
So X=(1.28155×20)+50=75.631
Therefore minimum score for exemplary employee is 76.