Question

Interactive Solution 6.39 presents a model for solving this problem. A slingshot fires a pebble from the top of a building at a speed of 20.0 m/s. The building is 25.0 m tall. Ignoring air resistance, find the speed with which the pebble strikes the ground when the pebble is fired (a) horizontally, (b) vertically straight up, and (c) vertically straight down.

Answer 1

(a) 29.8 m/s

To solve this problem, we start by analyze the vertical motion first. This is a free fall motion, so we can use the following suvat equation:

`v_y^2 - u_y^2 = 2as`

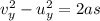
where, taking upward as positive direction:

`v_y` is the final vertical velocity

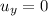`u_y = 0` is the initial vertical velocity (zero because the pebble is launched horizontally)

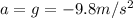`a=g=-9.8 m/s^2` is the acceleration of gravity

s = -25.0 m is the displacement

Solving for vy,

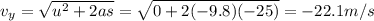`v_y = √(u^2+2as)=√(0+2(-9.8)(-25))=-22.1 m/s` (downward, so we take the negative solution)

The pebble also have a horizontal component of the velocity, which remains constant during the whole motion, so it is

`v_x = 20.0 m/s`

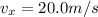
So, the final speed of the pebble as it strikes the ground is

`v=√(v_x^2+v_y^2)=√(20.0^2+(-22.1)^2)=29.8 m/s`

(b) 29.8 m/s

In this case, the pebble is launched straight up, so its initial vertical velocity is

`u_y = 20.0 m/s`

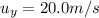
So we can find the final vertical velocity using the same suvat equation as before:

`v_y^2 - u_y^2 = 2as`

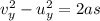
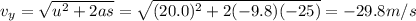`v_y = √(u^2+2as)=√((20.0)^2+2(-9.8)(-25))=-29.8 m/s` (downward, so we take the negative solution)

The horizontal speed instead is zero, since the pebble is initially launched vertically, so the final speed is just equal to the magnitude of the vertical velocity:

v = 29.8 m/s

(c) 29.8 m/s

This case is similarly to the previous one: the only difference here is that the pebble is launched straight down instead than up, therefore

`u_y = -20.0 m/s`

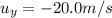
Using again the same suvat equation:

`v_y^2 - u_y^2 = 2as`

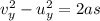
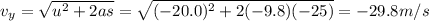`v_y = √(u^2+2as)=√((-20.0)^2+2(-9.8)(-25))=-29.8 m/s` (downward, so we take the negative solution)

As before, the horizontal speed instead is zero, since the pebble is initially launched vertically, so the final speed is just equal to the magnitude of the vertical velocity:

v = 29.8 m/s

We notice that the final value of the speed is always the same in all the three parts, so it does not depend on the direction of launching. This is due to the law of conservation of energy: in fact, the initial mechanical energy of the pebble (kinetic+potential) is the same in all three cases (because the height h does not change, and the speed v does not change either), and the kinetic energy gained during the fall is also the same (since the pebble falls the same distance in all 3 cases), therefore the final speed must also be the same.