Question

Line AB passes through points A(−6, 6) and B(12, 3). If the equation of the line is written in slope-intercept form, y=mx+b, then m=m equals negative StartFraction 1 Over 6 EndFraction.. What is the value of b? −6 −5 5 6

Answer 1

C) 5

Step-by-step explanation:

If m =
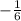`-(1)/(6)`, then y =
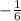`- (1)/(6)` x + b. If we substitute one of the points the line passes through into the equation as x and y, then we get
`3 = -(1)/(6) (12) + b`.
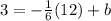`-(1)/(6) (12) = -2` so
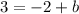`3 = -2 + b`. To isolate the variable, b, we move b to the left side of the equation by subtracting b from both sides. Now the equation is 3-b = -2. Next, subtract 3 from both sides so the equation is now -b = -2-3. Then just calculate the results. -2-3 = -5. Therefore, -b = -5. However, we can remove the negative signs because if b = 5, then -b = -5. So b = 5.

Answer 2

Answer: 5

Step-by-step explanation:

We can find our intercept b from the equation of the straight line:

y - y₁ = m (x-x₁ )

point A(-6, 6)

x₁ = -6 and y₁ =6

m= -1/6 (as stated in the question)

Inputing this values in our equation, we have;

y - 6 = -1/6 ( x - -6)

y - 6 = -1/6(x+6)

y - 6 = -1/6x -1

y = -1/6x - 1 + 6

y= -1/6x + 5

comparing y= mx+b with the equation above; b=5