Answer:
Maximum possible error is ±450
Uncertainty in absolute terms is ±318.1981
Relative terms is 1.4%
Step-by-step explanation:
Spring constant,
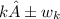 is 1500±15 N/cm and displacement,
is 1500±15 N/cm and displacement,
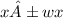 is 15±0.15cm
is 15±0.15cm
From first principles, k=F/x where F is force exerted on spring and x is displacement, k is spring constant
Taking k as 1500 and x as 15
F=kx=1500*15=22500N
The partial derivative of force with respect to k yields
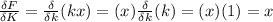
Therefore,
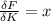 =15
=15
The partial derivative of force with respect to x yields
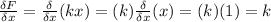
Therefore,
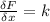 =1500
=1500
The maximum possible error for force
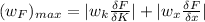
Substituting 15 for
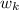 , 0.15 for
, 0.15 for
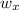 15 for
15 for
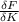 and 1500 for
and 1500 for
 for 1500
for 1500
 =±[(15)(15)+(0.15)(1500)]= ±[225+225]= ±450
=±[(15)(15)+(0.15)(1500)]= ±[225+225]= ±450
Therefore, maximum possible error is ±450
Uncertainty of measured force in absolute terms
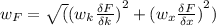
Substituting 15 for
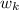 , 0.15 for
, 0.15 for
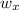 15 for
15 for
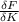 and 1500 for
and 1500 for
 for 1500
for 1500
![w_(F)=±\sqrt {[(15)(15)]^(2)+ [(0.15)(1500)]^(2)}=±\sqrt (50625+50625)](https://img.qammunity.org/2020/formulas/engineering/college/y0qgw128ch8g2msgntwwqb2g95l58wf1zy.png) = ±318.1981
= ±318.1981
Uncertainty in absolute terms is ±318.1981
Uncertainty of measured force in relative terms
Relative uncertainty =
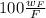
Since F is already calculated as 22500N and
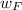 =±318.1981
=±318.1981
Relative uncertainty=
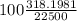 =1.414214%
=1.414214%
Therefore, measured force in relative terms is 1.4%