Question

A researcher compares the effectiveness of two different instructional methods for teaching anatomy. A sample of 66 students using Method 1 produces a testing average of 54.9. A sample of 110 students using Method 2 produces a testing average of 85.9. Assume that the population standard deviation for Method 1 is 6.04, while the population standard deviation for Method 2 is 16.44. Determine the 99% confidence interval for the true difference between testing averages for students using Method 1 and students using Method 2. Step 1 of 3 : Find the point estimate for the true difference between the population means.

Answer 1

99% confidence interval = [-35.47,-26.53]

Explanation:

For Method 1:

`n_1=66,\mu_1=54.9,\sigma_1=6.04`

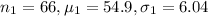
For Method 2:

`n_2=110,\mu_2=85.9,\sigma_2=16.44`

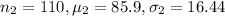
We need to find the 99% confidence interval for the true difference between testing averages for students using Method 1 and students using Method 2.

Step 1: Find the point estimate for the true difference between the population means.

`Difference=\mu_1-\mu_2`

`Difference=54.9-85.9`

`Difference=-31.0`

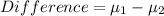
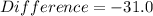
Therefore the point estimate for the true difference between the population means is -31.

Step 2: Find margin of error at 99% confidence.

From the standard normal table the critical value of z at 99% confidence = 2.576.

The formula for margin of error:

`M.E.=z^** \sqrt{(\sigma_1^2)/(n_1)+(\sigma_2^2)/(n_2)}}`

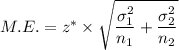
Substitute the values.

`M.E.=2.576* \sqrt{((6.04)^2)/(66)+((16.44)^2)/(110)}}`

`M.E.\approx 4.47`

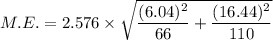
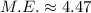
Therefore, the margin of error is 4.47.

Step 3: Find 99% confidence interval.

`C.I.=(\mu_1-\mu_2)\pm M.E.`

`C.I.=-31.0\pm 4.47`

`C.I.=-35.47,-26.53`

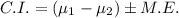
Therefore, the 99% confidence interval is [-35.47,-26.53].