Question

Provide a suitable domain and range to complete the definition of each function.

a. Let f(x) = 2x + 3.
b. Let f(x) = 2x.
c. Let C(x) = 9x + 130, where C(x) is the number of calories in a sandwich containing x grams of fat.
d. Let B(x) = 100(2)x, where B(x) is the number of bacteria at time x hours over the course of one day.

Answer 1

Explanation:

We have to find the domain and range of each function.

a.
`f(x)=2x+3`

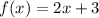
It is a linear function because the degree of function is 1.Linear function is defined for all real values of x.

Therefore, the domain of given function=R

When we substitute real values in the given function then we get again real values.

Therefore, range of f=R

b.
`f(x)=2x`

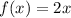
It is a linear function .

Domain=R

Range=R

c.
`C(x)=9x+130`

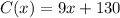
C(x)=Number of calories in a sandwich containing x grams of fat.

x=Mass of fat

Mass is always a natural number.

Domain of C=N

Substitute x=1

C(1)=9(1)+130=139

C(2)=9(2)+130=18+130=148

Range of C={139,148,157,...}

d.
`B(x)=100(2)^x`

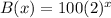
B(x)=Number of bacteria

x=Time in hours

Number of bacteria is a natural number and time is always a whole number.

Domain=W

Substitute x=0

`B(0)=100(2)^0=100`

`B(1)=100(2)^1=200`

`B(2)=100(2)^2=400`

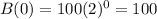
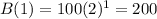
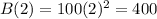
Range of B={100,200,200,800,...}