Answer:
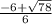 and
and
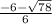
Explanation:
We are asked that what are the zeros of the quadratic function f(x) = 6x² +12x -7.
So, we have to find the roots of the equation, f(x) = 6x² +12x -7 =0 ...... (1)
Since the quadratic function can not be factorized, so we have to apply Sridhar Acharya's formula.
This formula gives if, ax² +bx +c =0, the the two roots of the equation are
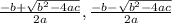
Therefore, in our case 'a' being 6, 'b' being 12 and 'c' being -7, the two roots of the equation (1) will be

=
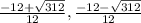
=
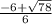 and
and
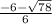
Hence, x=
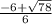
and x=
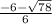
(Answer)