Question

. A professor surveyed the 98 students in her class to count how many of them had watched at least one of the three films in The Lord of the Rings trilogy. This is what she found: 74 had watched Part I . 57 had watched Part II . 66 had watched Part III 52 had watched both Parts I and II . 51 had watched both Parts I and III 45 had watched both Parts II and III; 43 had watched all three parts. How many students did not watch any one of these three movies?

Answer 1

6 students did not watch any one of these three movies.

Explanation:

To solve this problem, we must build the Venn's Diagram of this set.

I am going to say that:

-The set A represents the students that watched Part I.

-The set B represents the students that watched Part II.

-The set C represents the students that watched Part III.

-d is the number of students that did not watch any of these three movies.

We have that:

`A = a + (A \cap B) + (A \cap C) + (A \cap B \cap C)`

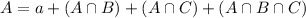
In which a is the number of students that only watched Part I,
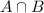`A \cap B` is the number of students that watched both Part I and Part II,
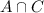`A \cap C` is the number of students that watched both Part I and Part III. And
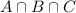`A \cap B \cap C` is the number of students that like all three parts.

By the same logic, we have:

`B = b + (B \cap C) + (A \cap B) + (A \cap B \cap C)`

`C = c + (A \cap C) + (B \cap C) + (A \cap B \cap C)`

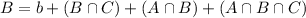
This diagram has the following subsets:

`a,b,c,d,(A \cap B), (A \cap C), (B \cap C), (A \cap B \cap C)`

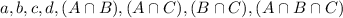
There were 98 students suveyed. This means that:

`a + b + c + d + (A \cap B) + (A \cap C) + (B \cap C) + (A \cap B \cap C) = 98`

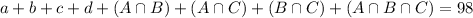
We start finding the values from the intersection of three sets.

43 had watched all three parts. This means that
`(A \cap B \cap C) = 43`.

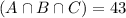45 had watched both Parts II and III. This means that:

`(B \cap C) + (A \cap B \cap C) = 45`

`(B \cap C) = 2`

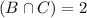
51 had watched both Parts I and III

`(A \cap C) + (A \cap B \cap C) = 51`

`(A \cap C) = 8`

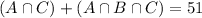
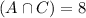
52 had watched both Parts I and II

`(A \cap B) + (A \cap B \cap C) = 52`

`(A \cap B) = 9`

66 had watched Part III

`C = 66`

`C = c + (A \cap C) + (B \cap C) + (A \cap B \cap C)`

`c + 8 + 2 + 43 = 66`

`c = 13`

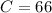
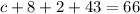
57 had watched Part II

`B = 57`

`B = b + (B \cap C) + (A \cap B) + (A \cap B \cap C)`

`b + 2 + 9 + 43 = 57`

`b = 3`

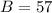
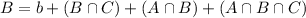
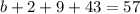
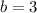
74 had watched Part I

`A = 74`

`A = a + (A \cap B) + (A \cap C) + (A \cap B \cap C)`

`a + 9 + 8 + 43 = 74`

`a = 14`

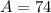
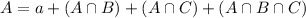
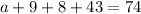
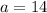
How many students did not watch any one of these three movies?

We have to find d.

`a + b + c + d + (A \cap B) + (A \cap C) + (B \cap C) + (A \cap B \cap C) = 98`

`14 + 3 + 13 + d + 9 + 8 + 2 + 43 = 98`

`d = 98 - 92`

`d = 6`

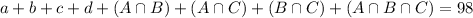
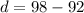
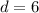
6 students did not watch any one of these three movies.