Question

A student examines 27 geological samples for nitrate concentration. The mean nitrate concentration for the sample data is 0.819 cc/cubic meter with a standard deviation of 0.0881. Determine the 90% confidence interval for the population mean lead concentration. Assume the population is approximately normal.

Step 1 of 2: Find the critical value that should be used in constructing the confidence interval. Round your answer to three decimal places. Construct the 90% confidence interval. Round your answer to three decimal places

Answer 1

Answer: 90% confidence interval: (0.790, 0.848)

Critical t- value for 90% confidence = 1.706

Explanation:

As we consider the given description, we hvae

n= 27

`\overline{x}=0.819`

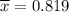
s=0.0881

Since population standard deviation is unknown.

so we use t-critical value

Using t-value table , the critical t- value will be:-

`t_(n-1,\ \alpha/2)=t_(26,\ 0.05)= 1.706`

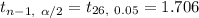
Confidence interval :
`\overline{x}\pm t_(n-1,\alpha/2)(s)/(√(n))`

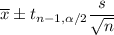
i.e.
`0.819\pm ( 1.706)(0.0881)/(√(27))`

`\approx0.819\pm 0.029=(0.819-0.029,\ 0.819+0.029)\\\\=(0.790,\ 0.848)`

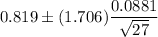
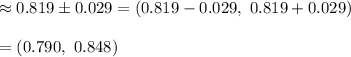
Hence, 90% confidence interval: (0.790, 0.848)