Question

Let λ > 0 be a constant. Consider the function f(x) = (λ/2)e^(−λ|x|) , for − [infinity] < x < [infinity] . (a) Is f(x) a pdf? Why? (b) If your answer is "yes" for part (a), find the corresponding µ and σ^2 (as simple functions of λ). If your answer is "no" for part (a), find the integral (from -[infinity] to [infinity]) of xf(x)dx and the integral(from -[infinity] to [infinity]) of x^2f(x)dx (as simple functions of λ).

Answer 1

a. In order for
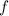`f` to be a PDF,
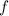`f` needs to be non-negative (it is) and the integral over its support must evaluate to 1.
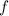`f` is symmetric about
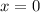`x=0`, i.e. even, so

`\displaystyle\int_(-\infty)^\infty\frac\lambda2e^(-\lambda|x|)\,\mathrm dx=\lambda\int_0^\infty e^(-\lambda x)\,\mathrm dx=-e^(-\lambda x)\bigg|_0^\infty=1`

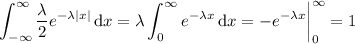
and so
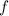`f` is indeed a PDF.

b. Let
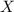`X` be a random variable with
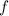`f` as its PDF. Then

`\mu=E[X]=\displaystyle\int_(-\infty)^\infty xf(x)\,\mathrm dx=\frac\lambda2\int_(-\infty)^\infty xe^(-\lambda|x|)\,\mathrm dx`

The integrand is odd, so the integral vanishes and the mean is
`\boxed{\mu=0}`.

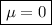The variance of
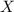`X` is

`\sigma^2=E[(X-E[X])^2]=E[X^2]-E[X]^2`

The second moment is

`E[X^2]=\displaystyle\int_(-\infty)^\infty x^2f(x)\,\mathrm dx`

This integrand is even, so

`E[X^2]=\displaystyle2\int_0^\infty x^2f(x)\,\mathrm dx=\lambda\int_0^\infty x^2e^(-\lambda x)\,\mathrm dx`

Integrate by parts, taking

`u=x^2\implies\mathrm du=2x\,\mathrm dx`

`\mathrm dv=e^(-\lambda x)\,\mathrm dx\implies v=-\frac{e^(-\lambda x)}\lambda`

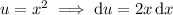
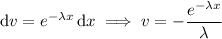
so that

`\displaystyle E[X^2]=\lambda\left(-\frac{x^2e^(-\lambda x)}\lambda\bigg|_0^\infty+2\int_0^\infty\frac{xe^(-\lambda x)}\lambda\,\mathrm dx\right)=2\int_0^\infty xe^(-\lambda x)\,\mathrm dx`

Integrate by parts again, this time with

`u=x\implies\mathrm du=\mathrm dx`

`\mathrm dv=e^(-\lambda x)\,\mathrm dx\implies v=-\frac{e^(-\lambda x)}\lambda`

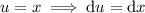
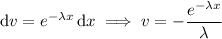
`\displaystyle E[X^2]=2\left(-\frac{xe^(-\lambda x)}\lambda\bigg|_0^\infty+\int_0^\infty\frac{e^(-\lambda x)}\lambda\,\mathrm dx\right)=\frac2\lambda\int_0^\infty e^(-\lambda x)\,\mathrm dx=-\frac2{\lambda^2}e^(-\lambda x)\bigg|_0^\infty=\frac2{\lambda^2}`

and so the variance is
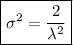`\boxed{\sigma^2=\frac2{\lambda^2}}`.