Answer:
Standard deviation = 2.16
Explanation:
Data provided:
7, 8, 10, 11, 8, 6, 10, 9, 9, 8, 13, 12, 8, 11, 11, 14, 8, 7, 10, and 12
Total number of observations, n = 20
Now,
Mean of the data =

or
Mean of the data =

or
Mean of the data = 9.6
Thus,
Observed value (x) value - Mean (Value - Mean)²
7 -2.6 6.76
8 -1.6 2.56
10 0.4 0.16
11 1.4 1.96
8 -1.6 2.56
6 -3.6 12.96
10 0.4 0.16
9 -0.6 0.36
9 -0.6 0.36
8 -1.6 2.56
13 3.4 11.56
12 2.4 5.76
8 -1.6 2.56
11 1.4 1.96
11 1.4 1.96
14 4.4 19.36
8 -1.6 2.56
7 -2.6 6.76
10 0.4 0.16
12 2.4 5.76
=====================================================
∑x = 192 ∑(Value - Mean)² = 88.8
Now,
Standard deviation =
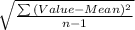
or
Standard deviation =
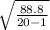
or
Standard deviation = 2.16