Question

A block of ice with mass 6.00 kg is initially at rest on a frictionless, horizontal surface. A worker then applies a horizontal force F⃗ to it. As a result, the block moves along the x-axis such that its position as a function of time is given by x(t)=( 0.199 m/s2 )t2+( 2.03×10−2 m/s3 )t3. Calculate the velocity of the object at time t=3.80s

Answer 1

`v=2.3918m/s`

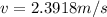
Step-by-step explanation:

From the exercise we know the block's equation of position

`x(t)=(0.199m/s^2)t^2+(2.03x10^(-2)m/s^3)t^3`

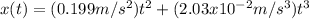
To calculate the velocity we need to derivate the equation of position

`v(t)=(dx)/(dt)`

`v(t)=2(0.199m/s^2)t+3(2.03x10^(-2)m/s^3)t^2`

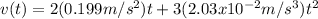
Now, we evaluate t=3.80s on the equation

`v(t=3.8s)=2(0.199m/s^2)(3.8s)+3(2.03x10^(-2)m/s^3)(3.8s)^2=2.3918m/s`

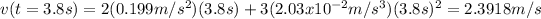
So, the block's velocity is 2.3918m/s at t=3.8s