Question

You are to take a multiple-choice exam consisting of 64 questions with 5 possible responses to each question. Suppose that you have not studied and so must guess (select one of the five answers in a completely random fashion) on each question. Let x represent the number of correct responses on the test. (a) What is your expected score on the exam? (Hint: Your expected score is the mean value of the x distribution.)(b) Compute the variance and standard deviation of x. Variance =Standard deviation =

Answer 1

(a) The expected score is 12.8

(b) The standard deviation is 3.2 and variance is 10.24

Explanation:

Consider the provided information.

You are to take a multiple-choice exam consisting of 64 questions with 5 possible responses to each question.

Here n=64 p=1/5 and q=1-1/5=4/5

Part (a) we need to find the expected score on the exam.

Expected = np

Expected score = number of questions × P(right)

`Score = 64 * (1)/(5) = 12.8`

Hence, the expected score is 12.8

Part (b) Compute the variance and standard deviation of x.

Standard Deviation:
`\sigma =√(npq)`

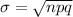
Now calculate the standard deviation as shown:

`\sigma =\sqrt{64* (1)/(5)* (4)/(5)}`

`\sigma =\sqrt{(256)/(25)}`

`\sigma =(16)/(5)=3.2`

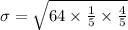
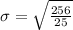
Variance:
`\sigma^2 =npq`

`\sigma^2 =64* (1)/(5)* (4)/(5)`

`\sigma^2 =(256)/(25)`

`\sigma^2 =10.24`

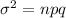
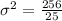
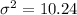
Hence, the standard deviation is 3.2 and variance is 10.24