Question

A force of 1.150×103 N pushes a man on a bicycle forward. Air resistance pushes against him with a force of 795 N. If he starts from rest and is on a level road, what speed ???? will he be going after 35.0 m? The mass of the bicyclist and his bicycle is 90.0 kg.

Answer 1

He has a speed of 16.60m/s after 35.0 meters.

Step-by-step explanation:

The final velocity can be determined by means of the equations for a Uniformly Accelerated Rectilinear Motion:

`v_(f)^(2) = v_(i)^(2) + 2ad`

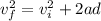
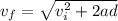`v_(f) = \sqrt{v_(i)^(2) + 2ad}` (1)

The acceleration can be found by means of Newton's second law:

`\sum F_(net) = ma`

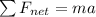
Where
`\sum F_(net)` is the net force, m is the mass and a is the acceleration.

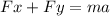`Fx + Fy = ma` (2)

All the forces can be easily represented in a free body diagram, as it is shown below.

Forces in the x axis:

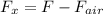`F_(x) = F - F_(air)` (3)

Forces in the y axis:

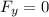`F_(y) = 0` (4)

Solving for the forces in the x axis:

`F_(x) = F - F_(air)`

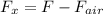
Where
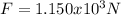`F = 1.150x10^(3) N` and
`F_(air) = 795 N`:

`F_(x) = 1.150x10^(3) N - 795 N`

`F_(x) = 355 N`

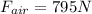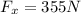
Replacing in equation (2) it is gotten:

`Fx + Fy = ma`

`355 N + 0 N = (90.0 Kg)a`

`355 N = (90.0 Kg)a`

`a = (355 N)/(90.0Kg)`

`a = (355 Kg.m/s^(2))/(90.0Kg)`

`a = 3.94 m/s^(2)`

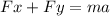
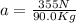
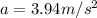
So the acceleration for the cyclist is
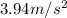`3.94 m/s^(2)`, now that the acceleration is known, equation (1) can be used:

`v_(f) = \sqrt{v_(i)^(2) + 2ad}`

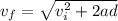
However, since he was originally at rest its initial velocity will be zero (
`v_(i) = 0`).

`v_(f) = √(2ad)`

`v_(f) = \sqrt{2(3.94m/s^(2))(35.0m)}`

`v_(f) = 16.60m/s`

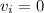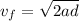
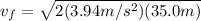
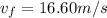
He has a speed of 16.60m/s after 35.0 meters