Question

Sequences are functions. The domain is the set of all term numbers (which is usually the positive integers), and the

range is the set of terms of the sequence. For example, the sequence 1, 4, 9, 16, 25, 36, … of perfect squares is the
function:
???? f:{positive integers} → {perfect squares}
Assign each term number to the square of that number.
a. What is f(3)? What does it mean?
b. What is the solution to the equation f(x) = 49? What is the meaning of this solution?
c. According to this definition, is −3 in the domain of f? Explain why or why not.
d. According to this definition, is 50 in the range of f? Explain why or why not.

Answer 1

Answer with Step-by-step explanation:

We are given that

`f:Z+\rightarrow` (perfect squares)

Assign each term number to the square of that number.

It can be write as

`f(x)=x^2` where
`x^2` is a perfect square number.

a.[/tex]f(3)=(3)^2=9[/tex]

It means that when we assign 3 then we get its corresponding perfect square number is 9.

b.
`f(x)=49`

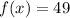
49 is a perfect square number and 49 is square of 7.

Therefore, x=7

7 is that number when we substitute in given function then we get perfect square number 49.

c.-3 is not in the domain of f because the domain of sequence is always a set of natural.

d.50 is not in the range of f because is 50 is not a square of any number .Therefore, 50 is not a square number.Hence, 50 is not in the range of f.