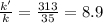Question

Tom has built a large slingshot, but it is not working quite right. He thinks he can model the slingshot like an ideal spring with a spring constant of 35.0 N/m.35.0 N/m. When he pulls the slingshot back 0.375 m0.375 m from a nonstretched position, it just does not launch its payload as far as he wants. His physics professor "helps" by telling him to aim for an elastic potential energy of 22.0 J.22.0 J. Tom decides he just needs elastic bands with a higher spring constant. By what factor does Tom need to increase the spring constant to hit his potential energy goal?

Answer 1

8.9

Step-by-step explanation:

We can start by calculating the initial elastic potential energy of the spring. This is given by:

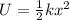`U=(1)/(2)kx^2` (1)

where

k = 35.0 N/m is the initial spring constant

x = 0.375 m is the compression of the spring

Solving the equation,

`U=(1)/(2)(35.0)(0.375)^2=2.5 J`

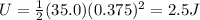
Later, the professor told the student that he needs an elastic potential energy of

U' = 22.0 J

to achieve his goal. Assuming that the compression of the spring will remain the same, this means that we can calculate the new spring constant that is needed to achieve this energy, by solving eq.(1) for k:

`k'=(2U')/(x^2)=(2(22.0))/(0.375^2)=313 N/m`

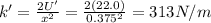
Therefore, Tom needs to increase the spring constant by a factor:

`(k')/(k)=(313)/(35)=8.9`