Question

Clem and Clyde have a farm with three different crops: a square field of corn, a rectangular field of artichokes, and a right-triangle grove of walnut trees (as shown at right). A fence totally surrounds the farm. Find the total area of Clem and Clyde's land in square miles and tell them how much fencing they need to enclose the outside of their farm.

Answer 1

The total area of the land is 4.4 square mi.

The length of the fence should be 9.2 mi.

Explanation:

Consider the provided information.

The required figure is shown below:

First, we need to find the Hypotenuse of the triangle by using the Pythagoras theorem.

`(\text{Hyp})^2=(1.6)^2+(1.2)^2`

`(\text{Hyp})^2=2.56+1.44`

`(\text{Hyp})^2=4`

`\text{Hyp}=2`

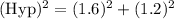
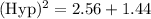
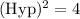
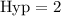
So, the hypotenuse of the triangle is 2 mi. Also, the hypotenuse of the triangle is the side of the rectangle.

Total area = Area of square + Area of Triangle + Area of rectangle

Total area =
`1.2* 1.2+(1)/(2)(1.2)(1.6)+2* 1`

Total area =
`1.44+0.96+ 2`

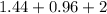
Total area = 4.4 square mi.

Now calculate the fencing they need to enclose the outside of their farm.

For this add the length of the red lines shown in the figure below:

`\text{Fence length outside the farm}=1.2+1.6+1+2+1+1.2+1.2`

`\text{Fence length outside the farm}=9.2`

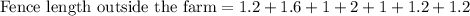
Hence, the length of the fence should be 9.2 mi.