Question

According to the South Dakota Department of Health, the number of hours of TV viewing per week is higher among adult women than adult men. A recent study showed women spent an average of 40 hours per week watching TV, and men, 34 hours per week. Assume that the distribution of hours watched follows the normal distribution for both groups, and that the standard deviation among the women is 4.7 hours and is 5.2 hours for the men.

a.
What percent of the women watch TV less than 43 hours per week? (Round z-score computation to 2 decimal places and your final answer to 4 decimal places.)


Probability
b.
What percent of the men watch TV more than 30 hours per week? (Round z-score computation to 2 decimal places and your final answer to 4 decimal places.)

Answer 1

Answer: a) 73.84%, b) 77.64%.

Explanation:

Since we have given that

Average number of hours women spent per week watching TV = 40

Standard deviation =4.7 hours

Average number of hours men spent per week watching TV = 34

Standard deviation = 5.2 hours

a. What percent of the women watch TV less than 43 hours per week? (Round z-score computation to 2 decimal places and your final answer to 4 decimal places.)

So, X is less than 43 hours.

So, we get that

`P(X<43)=P(Z<(43-40)/(4.7))=P(Z<0.64)=0.7384`

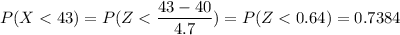
b. ) What percent of the men watch TV more than 30 hours per week? (Round z-score computation to 2 decimal places and your final answer to 4 decimal places.)

Since Y is more than 30 hours per week

So, it becomes

`P(Y>30)=P(Z>(30-34)/(5.2))=P(Z>-0.77)\\\\=0.5+P(0<Z<0.0.77)=0.5+0.2764=0.7764=77.64\%`

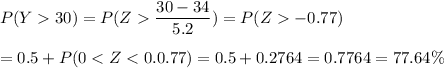
Hence, a) 73.84%, b) 77.64%.