The question mentions an illustration that is not provided, but I can solve the problem anyway.
Answer:
Ua - Ub = 5,390 J regardless of the reference height
Step-by-step explanation:
Gravitational Potential Energy
Gravitational potential energy is the energy stored in an object because of its vertical position or height in a gravitational field.
It can be calculated with the equation:
U=m.g.h
Where m is the mass of the object, h is the height with respect to a fixed reference, and g is the acceleration of gravity or
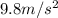 .
.
The problem is about proving the difference in potential energy does not depend on the reference used to calculate them.
a. Let's set the zero level for gravitational potential energy at B, i.e., h=0 at B.
The m=55 kg skier is at the top of the slope (point A) at a height of h=10 m.
The gravitational potential energy Ua is:
Ua = 55 * 9.8 * 10 = 5,390 J
The gravitational potential energy Ub (h=0) is:
Ub = 55 * 9.8 * 0 = 0 J
The difference is:
Ua - Ub = 5,390 J - 0 J = 5,390 J
b. Now fix the zero level at point A (h=0).
The gravitational potential energy Ua (h=0) is:
Ua = 55 * 9.8 * 0 = 0 J
Point B is at a height h=-10 m since it's below the reference.
The gravitational potential energy Ub (h=-10) is:
Ub = 55 * 9.8 * (-10) = -5,390 J
The difference is:
Ua - Ub = 0 J - (-5,390 J) = 5,390 J
We get the same value.
c. Finally, fix the reference at the midpoint between A and B.
Point A is at a height h=5 m since it's 5 m above the reference.
The gravitational potential energy Ua is:
Ua = 55 * 9.8 * 5 = 2695 J
Point B is at a height h=-5 m since it's 5 m below the reference.
The gravitational potential energy Ub is:
Ub = 55 * 9.8 * (-5) = -2695 J
The difference is:
Ua - Ub = 2695 J - (-2695 J) = 5,390 J
Again, we get the same value.
Conclusion:
Ua - Ub = 5,390 J regardless of the reference height